

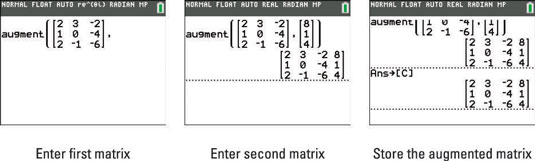
- #How to inser a matrix into a ti nspire cx cas program how to
- #How to inser a matrix into a ti nspire cx cas program archive
- #How to inser a matrix into a ti nspire cx cas program series
- #How to inser a matrix into a ti nspire cx cas program download
#How to inser a matrix into a ti nspire cx cas program archive
Gradient and directional derivatives This archive contains functions to calculate function gradients and directional derivatives. nocalc.zip: 16k: 10-11-04: No-Calc No-Calc is a revolutionary new training program for the TI-Nspire! It helps you train your calculating skills without using your. Functions are included for TI-nspire and 68k-models.
#How to inser a matrix into a ti nspire cx cas program series
Zipped File Updated Content calculus: : Gamma function, left, right, midpoint, trapezoidal sums, Simpson's Rule, partial fraction decomposition, second derivative, curvature : dseriescas: : Manually generate the terms of a series solution to 2nd order ODE (CAS only). Browse other questions tagged ti-nspire or ask your own question TI-Nspire Programs.
#How to inser a matrix into a ti nspire cx cas program how to
Take a look at the equation of the plane to see how to convert 'angle' into 'slope' So There is a way to use that easily? or I have to put manually the partial derivatives like new functions? I'm sorry for my english. You have control (sliders) for the angle of the plane (with the x-axis) and the z-intercept of the plane. (05/2011) A simple interactive file that uses the new 3D graphing capabilities of TI- Nspire. Finding Partial Derivatives With z1= x 3 + y 3 - 9xy, can be found on the TI-89 with the derivative commandĪ cone sliced by a plane. To find this partial derivative, take the derivative of z with respect to y while treating x as a constant. ain't a mathematician Similarly, is the partial derivative of z with respect to y. Just where is the limit of ability of the CAS system available. The problem is posed on the title screen shown at the right Just wondering if there is any derivative that the ti-nspire would mess up on. The Box_Problem_Calculus.tns document takes a classic problem from calculus and uses the dynamic linking capabilities of TI-Nspire to enact the problem in multiple representations: diagramatic, graphic, numeric, geometric, and symbolic. A template containing two fields is pasted to the entry line The Classic Box Problem - Calculus.

Press →Calculus→Derivative to open the Derivative command. The Derivative, Integral, and Limit commands form the cornerstone of the Calculus submenu on the TI-Nspire CAS. Just launch the Calculus Made Easy app at and select Multivariable Calculus in the menu: Now select Partial Derivatives and Gradient Enter the given Function and the given Point in the two top boxes Gradients and Partial Derivatives can be easily found using the Tinspire CX. The follow-up to this text is Calculus 2, which review the basic concepts of integration. This book contains numerous examples and illustrations to help make concepts clear. How To Do Partial Derivatives On Ti Nspire Cas APEX Calculus 1-Gregory Hartman A Calculus text covering limits, derivatives and the basics of integration.
#How to inser a matrix into a ti nspire cx cas program download
Title: How To Do Partial Derivatives On Ti Nspire Cas | Author: AN Whitehead - 2000 - Subject: Download How To Do Partial Derivatives On Ti Nspire Cas - On the last line, the quantities in square brackets are the real partial derivatives of uand v (with respect to x) Therefore those partial derivatives are well-de ned, and f0(z) = + i (23) On the.Partial Derivatives (TI-nSpire CX CAS) ptCSubscribe to my channel: that I wrote:https.
Finding Partial Derivatives using the TiNspire can easily be done using Calculus Made Easy at as follows: In the Menu select Multivariable Calculus, then select Partial Derivatives and Gradient: Next enter the given function using x and y as variables: The two partial.
Nevertheless, recall that to calculate a partial derivative of a function with respect to a specified variable, just find the ordinary derivative of the function while treating the other variables as constants


 0 kommentar(er)
0 kommentar(er)
